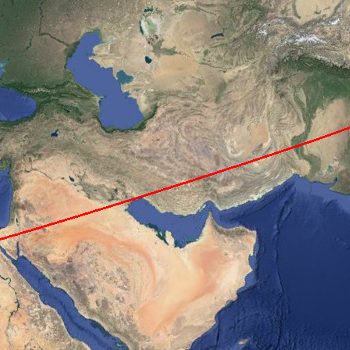
Según los seguidores de la teoría del «ecuador antiguo» (a falta de una denominación mejor) esta alineación sería evidencia de algún tipo de «gran plan oculto» que compartieron los constructores de estos sitios, quizás debido a que eran descendientes de una civilización perdida (los famosos atlantes) o inclusive gracias a algún tipo de «planificación planetaria» por parte de una civilización extraterrestre.

Este tema lo he encontrado planteado con pequeñas variantes en múltiples lugares, pero parecería que su forma más completa tiene origen en el artículo Exploring Geographic and Geometric Relationships Along a Line of Ancient Sites Around the World publicado por Jim Alison (del cual, por otra parte, no tengo más datos) en la web del conocido pseudo-investigador Graham Hancock. Alison va más allá y utiliza luego esta supuesta alineación para hacer un baile de números y relaciones… en este artículo no voy a aspirar a tanto y me voy a limitar a lo que más llama la atención al ojo desprevenido, eso es a la supuesta alineación en si misma.

Comprobando la alineación

La matemática nos dice que por un punto cualquiera pasan infinitas rectas, por lo que para definir una alineación se necesitan como mínimo dos puntos. Por cuestiones prácticas y porque son sitios de sobra conocidos, elegí como puntos de partida las Pirámides de Giza y la Isla de Pascua, trazando un gran círculo alrededor de la Tierra coincidente con ambos lugares.

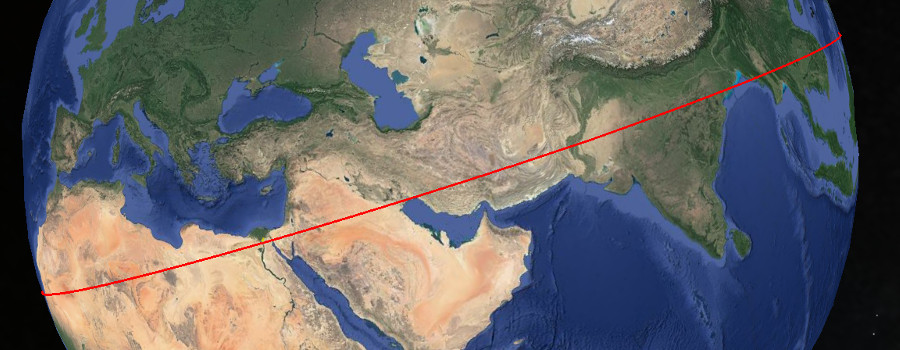
Si la teoría de la alineación es correcta, esta línea debería de pasar también por una multitud de otros lugares históricos: el geoglifo de Paracas, las líneas de Nazca, los sitios incas de Ollantaytambo, Machu Pichu y Sacsayuman, el arte rupestre en Tassili N’Ajjer, el oráculo de Amón en Siwa, las antiguas ciudades de Petra, Ur, Persepolis, Mohenjo Daro y Sukhothai y los templos de Khajuraho, Preah Vihear y Angkor Wat entre otros lugares supuestamente «especiales».

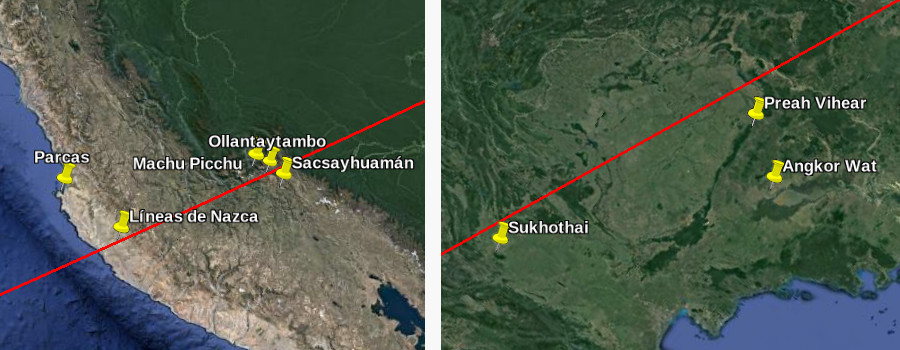
Cuando se incluyen las coordenadas de todos estos lugares en Google Earth (comprobando adicionalmente su posición de forma visual sobre el mapa), es evidente que la supuesta alineación no sucede. Aunque un puñado de los sitios mencionados si cae sobre la línea o por lo menos lo suficientemente cerca si se admite un pequeño margen de error (Google Earth no es perfecto y hace variar ligeramente la posición de la línea según el ángulo de visión), la mayoría quedan como mínimo a decenas de kilómetros… y algunos mucho más lejos. La antigua ciudad de Ur, por ejemplo, queda a 70 km al norte de la línea, y el geoglifo de Paracas se posiciona a 150 km en dicha dirección. Por otra parte, los templos de Preah Vihear y Angkor Wat se sitúan respectivamente a 85 km y 220 km al sur de la línea.

Así pues, tenemos resuelto que la «increíble, asombrosa y única» alineación no existe en realidad.
Se podría dejar el tema aquí, pero voy a jugar a ser abogado del diablo.

Aunque no estén alineados en una línea puntual, si parecen estar acotados a una franja relativamente estrecha, de unos 370 km de ancho. Si eliminamos los sitios más extremos (Paracas a 150 km al norte y Angkor Wat 220 km al sur) tenemos que el resto se posiciona en una franja de aprox. 155 km de ancho. Por puro argumento, supongamos que las medidas tomadas contienen un gran margen de error, por lo que reduzcamos la franja hasta los 100 Km de ancho (para usar números redondos). Comparar una franja de ese ancho con una línea puntual como lo es la línea del ecuador terrestre es evidentemente una enorme exageración, pero aún así es bastante impresionante, ¿no? Algo asombroso e inclusive ¿único?… no exactamente.

Evidencia incompleta o «cherry picking»

Llegados al punto en que tenemos una franja de sitios antiguos, cabe preguntarse… ¿y el resto de los sitios? Hay sitios antiguos mucho más famosos que los mencionados hasta ahora y que inclusive tienen mucha más relevancia entre los seguidores de las teorías atlantes o de contactos extraterrestres, que sin embargo quedan muy lejos de esta franja. Stonehenge, Tenochtitlan, Chichen Itzá o el Triángulo de las Bermudas, por citar algunos, quedan no ya a cientos sino a miles de km de distancia. Si el «ecuador antiguo» es realmente una zona tan importante y con tanto significado, ¿por qué todos estos lugares no se sitúan en esta «mágica» alineación? ¿por qué los antiguos egipcios construyeron un casi minúsculo templo a Amón en Siwa, pudiendo construir algo mucho más majestuoso, como el templo de Amón en Karnak? Cuando uno se enfrenta a estas preguntas de golpe se pierde gran parte de ese asombro inicial.

El asombro termina de esfumarse cuando se comprueba que el hecho supuestamente único es en realidad algo muy común, como se puede ver al hacer un experimento tan sencillo como lo es trazar una recta entre 2 puntos aleatorios del planeta, engordar esa línea para que pase a ser una franja de 100 km de ancho (¡recordar que estamos siendo generosos! Como vimos anteriormente en realidad la «línea del ecuador antiguo» representa una franja de 370 km) y ver que sitios quedan englobados. Todos esos sitios (que, recordemos, son determinados por 2 puntos elegidos de forma aleatoria) pasarían a estar tan alineados como los del «ecuador antiguo».

Con estos parámetros se pueden hacer infinitas «alineaciones», algunas de las cuales por pura estadística resultan hasta igual o más sorprendentes, por ejemplo la que involucra a un gran número de importantes ciudades europeas:

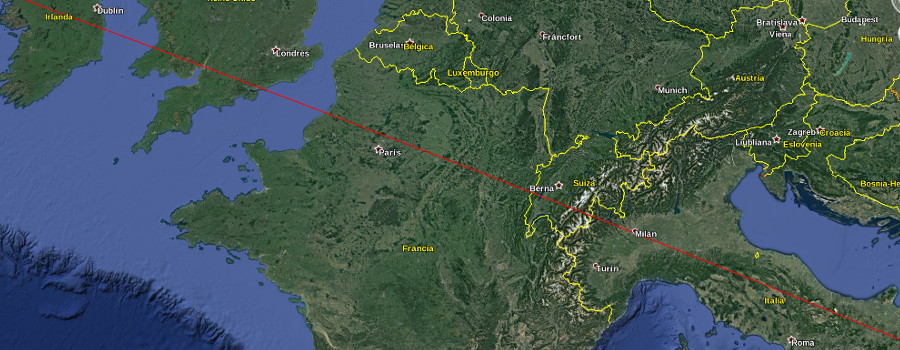
Elegir la parte de los datos que te da la razón e ignorar el resto se denomina falacia de evidencia incompleta aunque en inglés esto tiene un nombre más poético: «cherry picking«.

Como conclusión, estamos ante lo que en matemática se denomina, de forma humorística, el teorema del punto gordo y sus corolarios, «la recta gorda» y «la recta astuta»: una recta pasa por tres puntos no alineados siempre que ella o al menos uno de los puntos sea lo suficientemente gordo, o la recta lo suficientemente astuta.